Über unser Institut
Auf dem Gebiet der heterogenen Katalyse führen wir sowohl prozess- als auch grundlagenorientierte Untersuchungen an Zeolithen, geträgerten Metallkatalysatoren und redoxaktiven Oxiden sowie Oxidschichten durch. Diese werden am ITC hergestellt, charakterisiert und sorgfältig getestet.
Im Bereich chemische Reaktionstechnik führen wir prozess- und grundlagenorientierte, wissenschaftliche Untersuchungen zur technischen Reaktionskontrolle und zum Reaktordesign mit Schwerpunkt auf heterogener Katalyse, Mikroreaktionstechnik sowie elektrochemischer Reaktionstechnik durch. (Link zur Klemmgruppe).
Im Forschungsbereich molekulare, heterogene Katalyse (MHC) werden molekulare, wohl-definierte Katalysatoren synthetisiert, die auf Trägermaterialien immobilisiert werden können. Dies ermöglicht die Untersuchung von Struktur-Aktivitätsbeziehungen in der heterogenen Katalyse. Insbesondere nutzen wir MHC-Methoden, um die Ursachen von Strong Metal Support Interactions (SMSIs), Wechselwirkungen zwischen katalytisch aktiven Metallen und dem Trägermaterial, bei Reaktionen wie der CO2-Reduktion sowie der Mars-van-Krevelen Oxidation zu untersuchen.
Die Forschungsschwerpunkte am Institut für Technische Chemie

Säure/Base-Katalyse
Synthese von Zeolith-Katalysatoren; Charakterisierung; Festkörper-NMR
Anwendungsbeispiele: Dehydratisierungen von z.B. Milchsäure oder Ethanol; Dehydratisierungen in Kombination mit Amidierungen oder Oxidationen; Katalytisches Cracken von Bioölen; Methanol-to-Olefins
Oxidationskatalyse
Synthese von Mars-van-Krevelen-Katalysatoren, Monolayer-Katalysatoren und Metall-Träger-Katalysatoren; Charakterisierung; Isotherme reaktionstechnische Untersuchungen; Explosionsschutz
Anwendungsbeispiele: Selektivoxidationen von o-Xylol, n-Butan und Methan
Molekulare heterogene Katalyse
Oberflächen-Organometallchemie, Immobilisierung von molekularen Katalysatoren, Wechselwirkungen zwischen Metallen und Trägermaterialien
Anwendungsbeispiele: CO2-Hydrogenierung, Oxidationskatalyse, Hydrodeoxygenierung von Biomasse, Atomtransfer Reaktionen
Hydrierkatalyse
Metall-Träger-Katalysatoren; metallorganische Gerüstverbindungen; Charakterisierungen
Anwendungsbeispiele: Selektive Hydrierung von Alkinen zu Alkenen; Transferhydrierungen; CO2 Hydrierung
Mikroreaktionstechnik
Mikrofestbettreaktoren; Schlitzreaktoren mit Beschichtung; Mehrphasenreaktionen im Slug-Flow; Thermografie
Anwendungsbeispiele: Cyclohexan-Oxidation; Ethoxylierungen; Anionische Polymerisation von Butadien
Elektrochemische Reaktionstechnik
Gas-Diffusions-Elektroden; H-Typ-Zellen; Durchflusszellen; LSV; potentiostatische, galvanostatische Messungen
Anwendungsbeispiele: CO2-Reduktion zu Ameisensäure zur chemischen Speicherung und Substratversorgung von Fermentern; CO2-Reduktion zu Alkoholen
Neuigkeiten des ITC
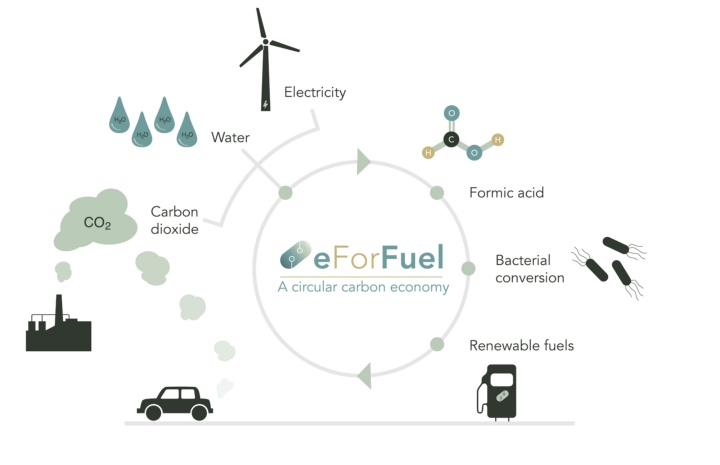
Sustainable CHEMical Production with Electricity
Universität Stuttgart beteiligt sich an eForFuel
Die Universität Stuttgart beteiligt sich an eForFuel, einer spannenden EU-finanzierten Forschung und Innovationsinitiative, die einen nachhaltigen Ersatz fossiler Brennstoffe durch Nutzung von Elektrizität und Mikroorganismen zur Umwandlung von CO2 in erneuerbare Kraftstoffe sucht.
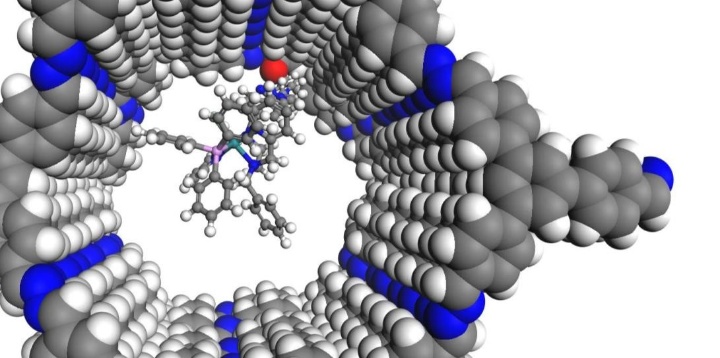
Das ITC im SFB 1333
Seit Juli 2022 läuft die zweite Förderperiode des SFB 1333 „Molekulare, heterogene Katalyse in definierten, dirigierenden Geometrien“ an der Universität Stuttgart. Am SFB 1333 sind die Estesgruppe sowie die Klemmgruppe am ITC mit drei verschiedenen Unterprojekten beteiligt. Im Rahmen dieser Projekte wird untersucht, wie sich poröse Trägermaterialien mit definierten, dirigierenden Geometrien auf die Aktivität und Selektivität der elektrokatalytischen und thermischen CO2-Reduktion auswirken und wie diese Materialien die Präkatalysator-Assoziation beeinflussen
Ihre Ansprechpartner

Elias Klemm
Prof. Dr.-Ing.Institutsleiter

Deven Estes
Jun.-Prof.Dr.Junior-Professor (TT W3)
Elisa Favaro
Assistenz der Institutsleitung